Part 15: Neural Networks

Kerry Back, Rice University

Overview

Neural networks are powerful machine learning models inspired by how neurons work in the brain. They learn to recognize patterns by adjusting internal parameters (weights and biases).

Key Concepts:

• Neurons: mathematical functions that transform inputs
• Layers: groups of neurons (input, hidden, output)
• Activation functions: non-linear transformations (sigmoid, ReLU)
• Training: optimizing weights/biases to minimize prediction error

Import Libraries

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
import warnings
warnings.filterwarnings('ignore')

np.random.seed(42)

Example Task: Digit Classification

Classify hand-written numbers (digits 0 through 9).

The original handwritten digits were pixelated into 64 pixels (8 x 8). Each observation consists of 65 numbers: the true digit and the darkness values of each of the 64 pixels. Darkness values range from 0 (white) to 16 (black).

Load and Explore the Digits Dataset

# Load the digits dataset
digits = load_digits()
X = digits.data  # 8x8 images flattened to 64 features
y = digits.target  # Digit labels 0-9

print(f"Digits Dataset:")
print(f"  Total samples: {X.shape[0]:,}")
print(f"  Features per sample: {X.shape[1]} (8×8 pixels)")
print(f"  Classes: {len(np.unique(y))} (digits 0-9)")
print(f"  Feature range: [{X.min():.1f}, {X.max():.1f}]")

Digits Dataset:
  Total samples: 1,797
  Features per sample: 64 (8×8 pixels)
  Classes: 10 (digits 0-9)
  Feature range: [0.0, 16.0]

Practice: Loading Data

Exercise 1 (with Gemini): Ask Gemini to “load the digits dataset from sklearn and print its shape”

Exercise 2 (on your own): Type from sklearn.datasets import load_digits then digits = load_digits() then print(digits.data.shape) and run it.

Visualize Sample Digits

fig, axes = plt.subplots(2, 10, figsize=(15, 4))

for digit in range(10):
    idx = np.where(y == digit)[0][0]
    axes[0, digit].imshow(X[idx].reshape(8, 8), cmap='gray_r')
    axes[0, digit].axis('off')

    idx2 = np.where(y == digit)[0][1]
    axes[1, digit].imshow(X[idx2].reshape(8, 8), cmap='gray_r')
    axes[1, digit].axis('off')

plt.suptitle('Two Examples Each of 0-9', fontsize=20, y=1.02)
plt.tight_layout()
plt.show()

Understanding Neural Networks: Simple Example

Generate customer data to predict purchase behavior:

• Input 1 (x1): Customer age (normalized)
• Input 2 (x2): Customer income (normalized)
• Target: 1 if customer purchases, 0 if not

Rule: customers usually purchase when age + income >= 0 (with noise)

Generate Customer Data

np.random.seed(42)
n_customers = 200

x1_age = np.random.uniform(-2, 2, n_customers)
x2_income = np.random.uniform(-2, 2, n_customers)

noise = np.random.normal(0, 1, n_customers)
true_score = x1_age + x2_income + noise
y_purchase = (true_score >= 0).astype(int)

customer_data = pd.DataFrame({
    'age_normalized': x1_age,
    'income_normalized': x2_income,
    'purchase': y_purchase
})

print("Customer Data Sample:")
print(customer_data.head())

Customer Data Sample:
   age_normalized  income_normalized  purchase
0       -0.501840           0.568127         1
1        1.802857          -1.663440         1
2        0.927976          -1.353485         1
3        0.394634           1.594217         1
4       -1.375925           0.425716         0

Practice: Generating Data

Exercise 1 (with Gemini): Ask Gemini to “generate random data with numpy and create a pandas DataFrame”

Exercise 2 (on your own): Type x = np.random.uniform(0, 1, 10) then print(x) and run it.

Visualize Purchase Behavior

plt.figure(figsize=(10, 8))
colors = ['red', 'blue']
labels = ['No Purchase', 'Purchase']

for i in [0, 1]:
    mask = y_purchase == i
    plt.scatter(x1_age[mask], x2_income[mask], c=colors[i], alpha=0.6,
               label=labels[i], s=50)

x_line = np.linspace(-2, 2, 100)
y_line = -x_line
plt.plot(x_line, y_line, 'k--', linewidth=2,
         label='Decision Boundary (age + income = 0)')

plt.xlabel('Age (normalized)')
plt.ylabel('Income (normalized)')
plt.title('Customer Purchase Behavior')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()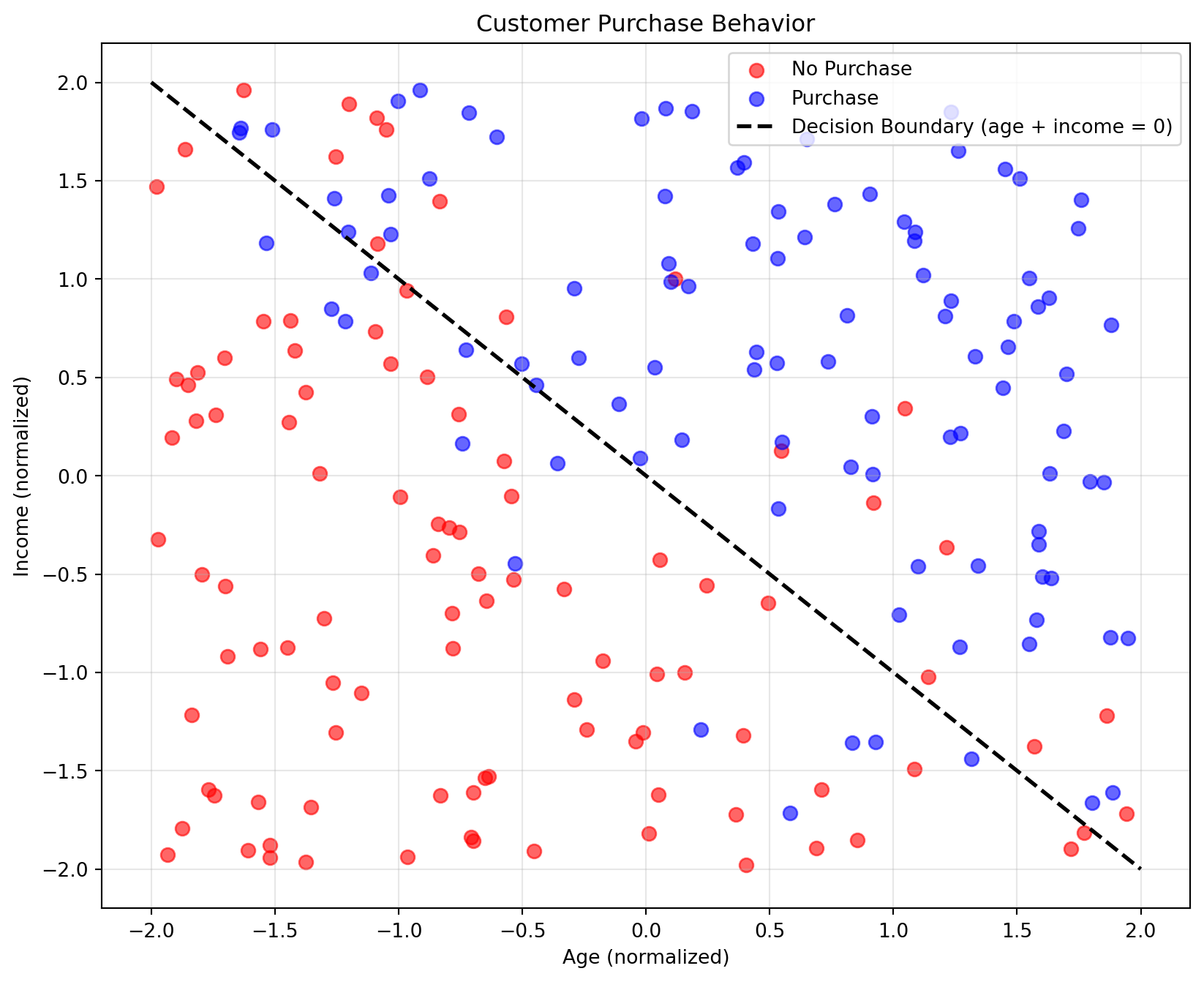

How Neurons Work

A neuron calculates a linear function then applies activation:

Linear Calculation: z = b + w1×x1 + w2×x2

• b = bias (intercept)
• w1, w2 = weights

Activation Functions:

• Sigmoid: h = 1/(1 + e^(-z)) outputs values in (0,1)
• ReLU: h = max(0, z) outputs values >= 0

The parameters (b, w1, w2) are learned from data during training.

Network Structure

Our simple network:

• Input layer: 2 inputs (x1, x2)
• Hidden layer: 3 neurons with sigmoid activation
• Output layer: 1 neuron with sigmoid activation

Parameters:

• Hidden layer: 3 biases + 3×2 weights = 9 parameters
• Output layer: 1 bias + 1×3 weights = 4 parameters
• Total: 13 parameters to optimize

Define Sigmoid Function

def sigmoid(z):
    """Sigmoid activation function: converts any real number to (0,1)"""
    z = np.clip(z, -500, 500)  # Prevent overflow
    return 1 / (1 + np.exp(-z))

Practice: Sigmoid Function

Exercise 1 (with Gemini): Ask Gemini to “write a Python function that implements the sigmoid activation function”

Exercise 2 (on your own): Type def sigmoid(z): return 1 / (1 + np.exp(-z)) then print(sigmoid(0)) and run it.

Example: Forward Propagation

# Network parameters (example values)
W1 = np.array([[0.5, 0.3], [-0.4, 0.6], [0.2, -0.3]])
b1 = np.array([0.1, -0.2, 0.3])
W2 = np.array([[0.7], [-0.5], [0.8]])
b2 = np.array([0.2])

# Example input
x_input = np.array([1.2, -0.8])

# Hidden layer calculation
z1 = W1 @ x_input + b1
h = sigmoid(z1)

# Output layer calculation
z2 = W2.T @ h + b2
y_hat = sigmoid(z2)[0]

print(f"Input: x1={x_input[0]}, x2={x_input[1]}")
print(f"Hidden: h1={h[0]:.3f}, h2={h[1]:.3f}, h3={h[2]:.3f}")
print(f"Output: y_hat={y_hat:.3f} ({y_hat:.1%} probability)")
print(f"Prediction: {'Purchase' if y_hat >= 0.5 else 'No Purchase'}")

Input: x1=1.2, x2=-0.8
Hidden: h1=0.613, h2=0.239, h3=0.686
Output: y_hat=0.742 (74.2% probability)
Prediction: Purchase

Practice: Forward Propagation

Exercise 1 (with Gemini): Ask Gemini to “explain how forward propagation works in a neural network with one hidden layer”

Exercise 2 (on your own): Type z = np.array([0.5, -0.3]) @ np.array([1.2, 0.8]) then print(z) and run it to practice matrix multiplication.

Summary

Neural Networks:

• Transform inputs through layers of neurons
• Each neuron applies weights, bias, and activation
• Parameters are optimized during training
• Can learn complex patterns in data

Next Steps:

• Use scikit-learn MLPClassifier for real applications
• Experiment with network architectures
• Try different activation functions
• Tune hyperparameters (learning rate, layers, neurons)